A Note on Multi-Level Hexagonal Grids

If I have a grid consisting of a large number of small squares I can group areas of squares together to make a coarser square grid, as in ordinary graph paper.

To do something analogous starting with a grid of small hexagons is not straightforward, and there is no single obvious way to proceed.

There are no long straight lines in a hexagonal grid, so I cannot build an exact large hexagon out of smaller ones. I can group small hexagons together to get an approximately hexagonal region, with zig-zag edges.

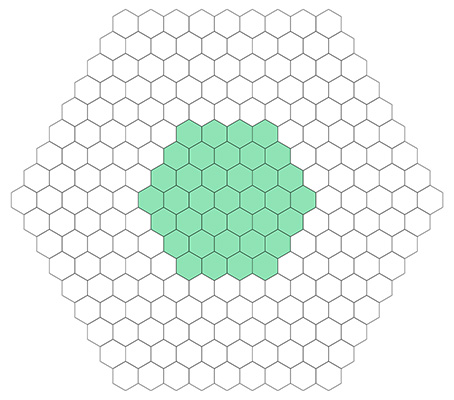
If I try to join hexagonal regions like these together along their edges, I end up with overlapping regions.

The solution I adopted was to have the hexagonal regions touch at their corners only, with triangular regions between the hexagonal ones.

This arrangement is an approximation to what is known as the "trihexagonal tiling".

I can repeat the arrangement of hexagonal and triangular regions at higher levels. It is quite hard to show in a diagram, but here is an attempt.

There are two levels of hexagonal regions. The larger regions (considered as below the smaller ones) are green, the small regions (superimposed on the larger ones) blue. Each larger green region has seven of the smaller blue regions sitting on top of it. The small white hexagonal cells are outside both the small (blue) and large (green) hexagonal regions.

In summary, I have an approximation to the trihexagonal tiling at every level of the multi-level grid. In The Limits to Growth I used four levels of hexagonal regions, and in Nanocosm six. Varying numbers of levels are used in some of the Hexa prints.